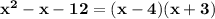Question

Factor the following expression[x squared minus x minus 12]

x2-x-12​

Answer 1

`x^2-x-12=(x-4)(x+3)`

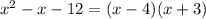
Explanation:

Factoring a Trinomial

A trinomial is expressed in the form

`ax^2+bx+c`

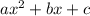
Where a,b, and c are real constants.

Some trinomials can be factored as the product of binomials with real coefficients, while others cannot.

If possible, factoring can be done in several ways:

• Factoring out the GCF.
• The sum-product pattern (by inspection).
• The grouping method.
• The perfect square trinomial pattern.
• The difference of squares pattern.
• Knowing the roots

Each method is most likely applicable under certain circumstances. When the polynomial has a leading coefficient of a=1, the sum-product pattern is the fastest and easiest option.

We have the polynomial

`x^2-x-12`

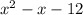
Here: a=1, b=-1, c=-12

The sum-product method needs us to find two numbers which sum is -1 and product is -12. Those numbers can be found by inspection by combining two divisors of 12, say 1 and 12, 2 and 6, or 3 and 4.

Only one of those pairs can be combined to produce a sum or subtraction equal to -1: Those numbers are -4 and 3. Thus the factorization is:

`\mathbf{x^2-x-12=(x-4)(x+3)}`