Question

please help :( I know that
`2^(6)/(5)` is the same as
`2\sqrt[5]{2}` but I don't understand how to get
`2\sqrt[5]{2}` from
`2^(6)/(5)`

Answer 1

`\displaystyle 2^{(6)/(5)}=2\sqrt[5]{2}`

Explanation:

Fractional Exponents

An expression like

`\displaystyle a^{(n)/(m)}`

can be expressed as a radical of the form:

`\sqrt[m]{a^n}`

We have the expression:

`\displaystyle 2^{(6)/(5)}`

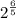
Its equivalent radical form is:

`\displaystyle 2^{(6)/(5)}=\sqrt[5]{2^6}`

Since the exponent is greater than the index of the radical, we can take 2 out of it by following the procedure:

`\sqrt[5]{2^6}=\sqrt[5]{2^5\cdot 2}`

Taking out
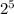`2^5` from the radical:

`\sqrt[5]{2^6}=2\sqrt[5]{2}`

Thus:

`\displaystyle 2^{(6)/(5)}=2\sqrt[5]{2}`