Answer:
Depends.
If you defined
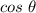 and
and
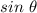 based on the unit circle, as in the coordinates of the point at a distance of
based on the unit circle, as in the coordinates of the point at a distance of
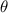 from the point
from the point
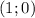 measured counterclockwise along the circle, then. it's proven by the fact that since that points sit on a circle of center the origin and radius 1, it's coordinates needs to satisfy the equation
measured counterclockwise along the circle, then. it's proven by the fact that since that points sit on a circle of center the origin and radius 1, it's coordinates needs to satisfy the equation
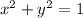 .
.
If you define them based on right triangles, as in the ratios between adjacent (cosine) or oppsite (sine) sides and the hypotenuse, then it's simply applying the Pythagorean theorem. In particular let a be the hypotenuse of a right triangle of which one of the angles measures
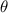 , let b the adjacent side to said angle, and c the opposite side.
, let b the adjacent side to said angle, and c the opposite side.
By definition,
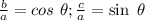 . clearing denominators we get
. clearing denominators we get
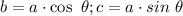 , and applying the Pythagorean theorem:
, and applying the Pythagorean theorem:
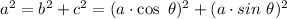 And, taking the first and last step in this chain, dividing everything by
And, taking the first and last step in this chain, dividing everything by
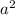 which is obviously non-zero we're left with
which is obviously non-zero we're left with
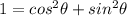 , QED.
, QED.