Question

The sum of vectors A with the length 4 units and B with the length 8 units is perpendicular to A. What is the angle in degrees) between A and B?

Answer 1

The angle between vectors A and B is 116.6°.

Step-by-step explanation:

Geometric Addition of Vectors

The geometric construction of the situation stated in the question is shown in the image below.

The angle between vectors A and B is the sum of 90° and θ.

Angle θ can be found by working on the right triangle of side lengths 8 and 4, and angle θ.

We use the tangent ratio:

`\displaystyle \tan\theta=\frac{\text{opposite leg}}{\text{adjacent leg}}`

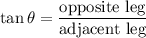
The opposite leg to θ is 4 and the adjacent leg is 8, thus:

`\displaystyle \tan\theta=(4)/(8)=(1)/(2)`

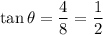
Calculating the angle:

`\displaystyle \theta=\arctan\left((1)/(2)\right)`

`\theta\approx 26.6^\circ`

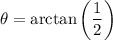
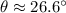
Thus the required angle is 90° + 26.6° = 116.6°

The angle between vectors A and B is 116.6°.