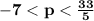Question

Please help me

Solve the inequality and show step by step

|-2-10p|+2<70

Answer 1

solving the inequality
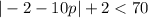`|-2-10p|+2<70` we get
`\mathbf{-7 < p < (33)/(5)}`

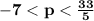
Explanation:

We need to solve the inequality

`|-2-10p|+2<70`

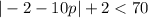
Step 1: Subtract 2 from both sides

`|-2-10p|+2-2<70-2\\|-2-10p|<68`

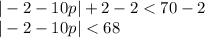
Step 2: Using the rule |u| < a then -a < u < a

`-68<-2-10p<68`

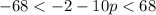
Step 3: Solving:

`-2-10p >-68 \ or \ -2-10p < 68\\-10p >-68+2 \ or \ -10p < 68+2\\-10p >-66 \ or \ -10p < 70`

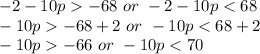
Step 4: Divide both sides by -10, the inequalities will be reversed

`(-10p)/(-10)<(-66)/(-10) \ or \ (-10p)/(-10)>(70)/(-10)\\p<(33)/(5) \ or \ p>-7`

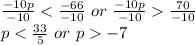
Step 5: Combining the terms

`-7 < p < (33)/(5)`

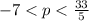
So, solving the inequality
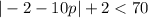`|-2-10p|+2<70` we get
`\mathbf{-7 < p < (33)/(5)}`