Answer:
The standard form of the equation is:
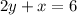
Hence, option B is true.
Explanation:
Given
We know the point-slope of the line equation is

where m is the slope of the line and (x₁, y₁) is the point
substituting the values m = -1/2 and the point (-4, 5) in the point-slope form

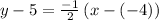
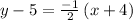
Add 5 to both sides


Writing the equation in the standard form form
As we know that the equation in the standard form is
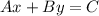
where x and y are variables and A, B and C are constants
so


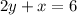
Thus, the standard form of the equation is:
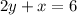
Hence, option B is true.