Answer:

Explanation:
The discriminant is the portion of the Quadratic Formula that is under a square root. It helps us identify if a function has 2,1, or 0 solutions.
The quadratic formula is:

where the quadratic is: ax²+bx+c
The part under the square root is just:
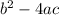
We are given the quadratic:
x² -3x+18
Therefore,
- a= 1 (there is an implied coefficient of 1 in front of the x²)
- b= -3
- c= 18
Substitute the values into the formula for the discriminant.
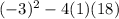
Solve the exponent.
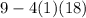
Multiply.

Subtract
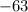
Since the discriminant is negative, there are no real solutions. There are imaginary solutions though.