Answer:
4) c = 10
5) b = 10
6) b = 12
7) a = 4
Explanation:
Pythagorean Theorem = a^2 + b^2 = c^2
to solve these, just substitute a, b, and c for the values given.
4) a = 8, b = 6
a^2 + b^2 = c^2
8^2 + 6^2 = c^2
64 + 36 = c^2
100 = c^2
c =
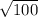
c = 10
5) a = 24, c = 26
a^2 + b^2 = c^2
24^2 + b^2 = 26^2
576 + b^2 = 676
subtract 576 from both sides
b^2 = 676 - 576
b^2 = 100
b = 10
6) a = 5, c = 13
a^2 + b^2 = c^2
5^2 + b^2 = 13^2
25 + b^2 = 169
subtract 25 from both sides
b^2 = 169 - 25
b^2 = 144
b = 12
7) b = 11, c =
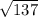
a^2 + b^2 = c^2
a^2 + 11^2 = 137
a^2 + 121 = 137
a^2 = 137 - 121
a^2 = 16
a = 4