Question

Two vertical poles, one 8 feet high and the other 10 feet high, stand 50 feet apart on a flat surface. We want to attach a support wire to each poles by running wire from the ground to the top of each pole. If we are to stake both wires into the ground at the same point, where should the stake be placed to use the least amount of wire?

Answer 1

Answer: amount of wire needed is 5.84 feet.

Explanation:

given data:

height of the first pole = 8 feet

height of the second pole = 10 feet

distance between both poles = 50 feet

SOLUTION:

L1 =
`\sqrt{x^(2) + 8^(2) } \\`

=
`\sqrt{x^(2) + 64}`

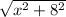
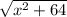
L2 =
`\sqrt{(50-x)^(2) +10^(2) }`

=
`\sqrt{(50-x)^(2)+100 }`

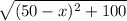
total length of wire

L = L1 + L2

L =
`\sqrt{x^(2) + 64}+\sqrt{(50-x)^(2)+100 }`

`(dL)/(dx)=(2x)/(2\sqrt x^(2) +64) + \frac{2(50-x(-1)}{2\sqrt{(50-x)^(2) +100} } =0`

`(x)/(\sqrt x^(2) +64) = (50-x)/(√((50-x)+100) )`

`x√((50-x) )^(2)+100 = (50-x)\sqrt{x^(2) +64}`

`x^(2) ((50-x)+100)=(15-x)^(2) (x^(2) +64)`

`x^(2) (50-x)^(2) +100x^(2) =x^(2) (50-x)^(2) +64(50-x)^(2) \\\\100x^(2) = 64(50-x)^(2) \\100x^(2) =64((50-x)(50-x))\\100x^(2) = 64(2500-100x+x^(2) )\\\\100^(2) =160000 -6400x+64x^(2) \\\\36x^(2) +6400x-160000=0`

`36x^(2) + 64x-1600=0`

`18x^(2) +32x+800=0`

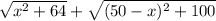
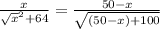
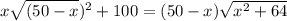
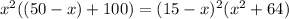
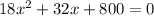
using quadratic equation

`a=18\\b=32\\c=800\\`

refer to the attached image

`x=(-8)/(9) +(4)/(9) √(229) \\or \\x=x=(-8)/(9) +(-4)/(9) √(229)`

`x = 5.84\\or\\x= -7.61`