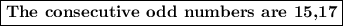Answer:
15,17
Explanation:
Let the two consecutive odd numbers be (2x + 1) and 2x + 3
Twice the greater number : 2* (2x + 3) = 2*2x + 2*3
= 4x + 6
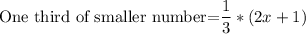
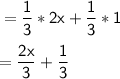
Difference = 29
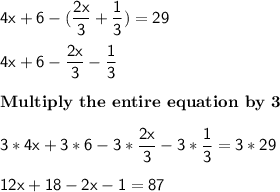
Combine the like terms.
12x - 2x + 18 - 1 = 87
10x + 17 = 87
Subtract 17 from both sides
10x = 87 - 17
10x = 70
Divide both sides by 10
x = 70/10
x = 7
2x + 1 = 2*7 + 1
= 14 + 1
= 15
2x + 3 = 2*7 + 3
= 14 + 3
= 17