Answer:
El alemán debe recorrer de la ciudad B a la ciudad A para llevar los cilindros de gas de cloro.
Explanation:
De acuerdo con este problema, tenemos un ángulo y dos lados adyacentes, por tanto, podemos determinar la distancia entre las ciudades A y B, medida en kilómetros, por la Ley del Coseno, definida como sigue:
 (1)
(1)
Donde:
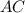 - Distancia entre las ciudades A y C, medida en kilómetros.
- Distancia entre las ciudades A y C, medida en kilómetros.
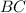 - Distancia entre las ciudades B y C, medida en kilómetros.
- Distancia entre las ciudades B y C, medida en kilómetros.
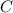 - Ángulo en la ciudad C, medida en grados sexagesimales.
- Ángulo en la ciudad C, medida en grados sexagesimales.
Si tenemos que
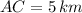 ,
,
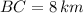 y
y
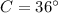 , entonces:
, entonces:
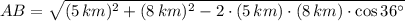
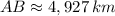
El alemán debe recorrer de la ciudad B a la ciudad A para llevar los cilindros de gas de cloro.