Answer:
see explanation
Explanation:
1
An extraneous solution tend to occur when dealing with equations involving radicals or absolute value functions.
Solutions are obtained by solving the equation and then must be verified by substituting them into the original equation.
Although a simplified solution is obtained it may not satisfy the original equation and is therefor extraneous.
2
It is the power that the value is being raised to
For example
rule of exponents
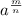 ⇔
⇔
![\sqrt[m]{a^(n) }](https://img.qammunity.org/2021/formulas/mathematics/college/t9t9evtp9fpyr8pg5jpgwdl77tacew1162.png)
3
A complex number does not appear on the set of real numbers.
It is composed of a real part and an imaginary part, usually in the form
z = a + bi ( where a and b are real )
a is the real part and bi the imaginary part
They are based on
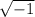 = i
= i
We can then solve problems involving negative radicals, particularly in solving quadratic equations
x = ±
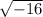 = ±
= ±
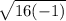 = ±
= ±
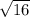 ×
×
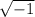 = ± 4i
= ± 4i