Recall that tangent is the ratio of sine over cosine
tan = sin/cos
This means we'll have sin(theta+2pi) up top and cos(theta+2pi) in the bottom
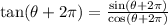
Now because both sine and cosine have a period of 2pi, this means,
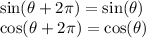
The graph of each repeats itself every 2pi units, which is why we're back to the original version of each.
So,
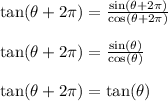
This seems to suggest that tangent also has a period of 2pi. This is false or misleading. It turns out the period of tangent is pi. The proof of this is a bit more involved. See the screenshot below to see those steps.