Answer:
Smaller acute angle measures 16°.
Explanation:
Calculate each angle by using trigonometric functions.
Step 1: Draw the right triangle.
See attached picture. Hypotenuse is always across the 90° angle and for the leg (which is 7) doesn't matter which of the drawn legs you choose. The two acute angles are x and y.
Step 2: Calculate angles.
We know that:
AB = 7 (leg)
CB = 25 (hypotenuse)
Calculate x.
From the reference angle x AB is adjacent and CB hypotenuse.
Recall SOH CAH TOA - SineOppositeHypotenuse CosineAdjacentHypotenuse TangentOppositeAdjacent
We have adjacent and hypotenuse so let's use cosine.
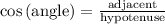
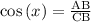
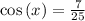
To get the angle x use function
 on calculator. (arccos)
on calculator. (arccos)
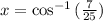
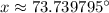
Rounded to nearest degree:
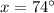
Calculate y.
From the reference angle x AB is opposite and CB hypotenuse, so we can use sine.
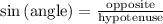
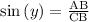
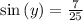
To get the angle y use function
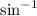 on calculator. (arcsin)
on calculator. (arcsin)


Rounded to nearest degree:

Smaller acute angle measures 16°.
---
You could also calculate only one angle and use the fact that the sum of the angles in triangle is 180°.
x + y + 90° = 180°
But if you choose this approach make sure to not round too much in between and do that only at the end. So if you calculated x use 73.7398° or more decimals (more is even more accurate and better) and round to the nearest degree only in the end.