Question

The function C(x)=−20x+1681 represents the cost to produce x items. What is the least number of items that can be produced so that the average cost is no more than $21?

Answer 1

The least number of items to produce is 41

Explanation:

Average Cost

Given C(x) as the cost function to produce x items. The average cost is:

`\displaystyle \bar C(X)=(C(x))/(x)`

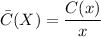
The cost function is:

`C(x) = -20x+1681`

And the average cost function is:

`\displaystyle \bar C(X)=(-20x+1681)/(x)`

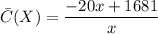
We are required to find the least number of items that can be produced so the average cost is less or equal to $21.

We set the inequality:

`\displaystyle (-20x+1681)/(x)\le 21`

Multiplying by x:

`-20x+1681 \le 21x`

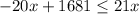
Note we multiplied by x and did not flip the inequality sign because its value cannot be negative.

Adding 20x:

`1681 \le 21x+20x`

`1681 \le 41x`

Swapping sides and changing the sign:

`41x \ge 1681`

Dividing by 41:

`x\ge 41`

The least number of items to produce is 41