Question

If anyone knows about definite integrals for calculus then please I request help! I

Will award 100 points to anyone who can figure out the answer in RED! THANKS AND GOOD LUCK!!

Answer 1

`\displaystyle \int\limits^9_5 {(1)/(x^3)e^\big{4x^(-2)}} \, dx = (1)/(8) \bigg( e^\Big{(4)/(25)} - e^\Big{(4)/(81)} \bigg)`

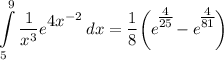
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Integration

• Integrals

Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

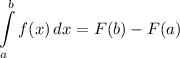
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

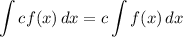
U-Substitution

Explanation:

Step 1: Define

Identify

`\displaystyle \int\limits^9_5 {(1)/(x^3)e^\big{4x^(-2)}} \, dx`

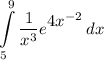
Step 2: Integrate Pt. 1

Identify variables for u-substitution.

1. Set u:
   `\displaystyle u = 4x^(-2)`
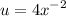
2. [u] Differentiate [Basic Power Rule, Derivative Properties]:
   `\displaystyle du = (-8)/(x^3) \ dx`
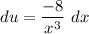
3. [Bounds] Switch:
   `\displaystyle \left \{ {{x = 9 ,\ u = 4(9)^(-2) = (4)/(81)} \atop {x = 5 ,\ u = 4(5)^(-2) = (4)/(25)}} \right.`

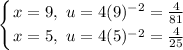
Step 3: Integrate Pt. 2

1. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int\limits^9_5 {(1)/(x^3)e^\big{4x^(-2)}} \, dx = (-1)/(8)\int\limits^9_5 {(-8)/(x^3)e^\big{4x^(-2)}} \, dx`
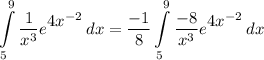
2. [Integral] U-Substitution:
   `\displaystyle \int\limits^9_5 {(1)/(x^3)e^\big{4x^(-2)}} \, dx = (-1)/(8)\int\limits^{(4)/(81)}_{(4)/(25)} {e^\big{u}} \, du`
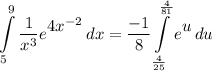
3. [Integral] Exponential Integration:
   `\displaystyle \int\limits^9_5 {(1)/(x^3)e^\big{4x^(-2)}} \, dx = (-1)/(8)(e^\big{u}) \bigg| \limits^{(4)/(81)}_{(4)/(25)}`
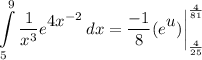
4. Evaluate [Integration Rule - Fundamental Theorem of Calculus 1]:
   `\displaystyle \int\limits^9_5 {(1)/(x^3)e^\big{4x^(-2)}} \, dx = (-1)/(8) \bigg( e^\Big{(4)/(81)} - e^\Big{(4)/(25)} \bigg)`
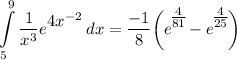
5. Simplify:
   `\displaystyle \int\limits^9_5 {(1)/(x^3)e^\big{4x^(-2)}} \, dx = (1)/(8) \bigg( e^\Big{(4)/(25)} - e^\Big{(4)/(81)} \bigg)`

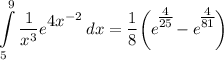
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration