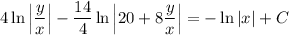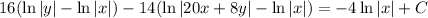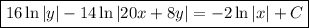The given differential equation
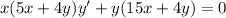
is indeed homogeneous, since we can write

Let
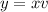 , so that
, so that
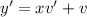 . Then
. Then
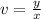 and the equation transforms to
and the equation transforms to
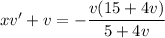
Rewrite a bit and separate the variables:
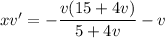
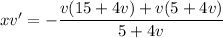

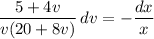
Integrate both sides. On the left, take the partial fraction decomposition,
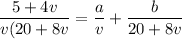
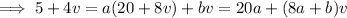
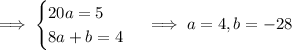
Proceed with the integrals.
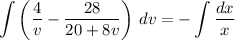
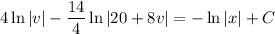
Get the solution back in terms of
 and
and
 .
.