(See screenshot for the first step that I *would* include, but apparently the website thinks it contains profanity...)
Now recall the following properties of logarithms:
•
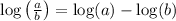
•
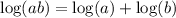
•
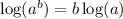
By the first property,
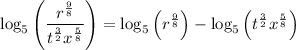
By the second property,
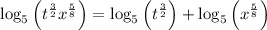
By the third property,
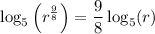

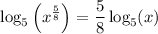
Putting everything together, we get the expanded expression
![\log_5\left(\sqrt[8]{(r^9)/(t^(12)x^5)}\right) = \frac98\log_5(r) - \left(\frac32\log_5(t) + \frac58\log_5(x)\right)](https://img.qammunity.org/2021/formulas/mathematics/high-school/t1six7noohff1l1o389fua3u0uchuf7k9w.png)
Now just plug in the given values to get
![\log_5\left(\sqrt[8]{(r^9)/(t^(12)x^5)}\right) = \boxed{9.97}](https://img.qammunity.org/2021/formulas/mathematics/high-school/q046vc0ti3z62uvk6uwrn95xg6kvij36h8.png)