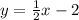Answer:
- The equation of the line is:
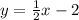
Explanation:
Given the points
Finding the slope between two points
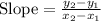
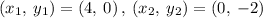

We know that the y-intercept can be obtained by setting the value x=0 and solving for y.
From the graph, it is clear that at x=0, the value of y = -2
Thus, the y-intercept (b) = -2
We know that the slope-intercept form of the line equation is

where m is the slope and b is the y-intercept.
Substituting m=1/2 and y-interept (b) = -2 in the slope-intercept form of the line equation

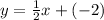
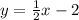
Thus, the equation of the line is: