Answer:
The y-intercept of the function is: b=10
Explanation:
Given the table
x y
1 8
2 6
3 4
4 2
Taking any two points to find the slope
The slope between (1, 8) and (2, 6) is:
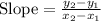
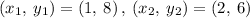
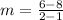

We know that the slope-intercept form of the line equation is

where m is the slope and b is the y-intercept.
Substituting m=-2 and any point i.e. (1, 8) in the slope-intercept form of the line equation to find the y-intercept (b).

8 = -2(1) + b
8 = -2 + b
b = 8+2
b = 10
Thus, the y-intercept of the function is: b=10