Answer:
1) The factors of
 are
are
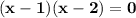
Option C is correct.
3) The factors of
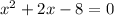 are
are
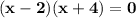
Option B is correct.
Explanation:
1) Factor :

For factoring we need to break the middle term, such that there sum is equal to middle term of expression and product is equal to product of first and last term.
The middle term : -3x
We can break them as (-2x)( -x)
Solving:

So, factors of
 are
are
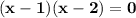
Option C is correct.
3) Factor:
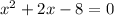
For factoring we need to break the middle term, such that there sum is equal to middle term of expression and product is equal to product of first and last term.
The middle term : 2x
We can break them as (4x)( -2x)
Solving
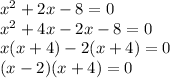
So, factors of
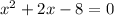 are
are
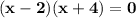
Option B is correct.