Question

you have a total of 21 coins that are nickels and quarters. the total is $3.25. How many nickels do you have? and quarters?

Answer 1

There are 10 nickels and 11 quarters in the jar.

Explanation:

Given that:

Total coins = 21

Total value = $3.25 = 3.25*100 = 325 cents

One nickel = 5 cents

One quarter = 25 cents

Let,

x be the number of nickels

y be the number of quarters

According to given statement;

x+y=21 Eqn 1

5x+25y=325 Eqn 2

Multiplying Eqn 1 by 5

5(x+y=21)

5x+5y=105 Eqn 3

Subtracting Eqn 3 from Eqn 2

(5x+25y)-(5x+5y)=325-105

5x+25y-5x-5y=220

20y=220

Dividing both sides by 20

`(20y)/(20)=(220)/(20)\\y=11`

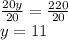
Putting y=11 in Eqn 1

x+11=21

x=21-11

x=10

Hence,

There are 10 nickels and 11 quarters in the jar.