Question

What is the slope of the line parallel to y=2/5x-1?
I really need help with this fast please

Answer 1

The slope will be 2/5.

Explanation:

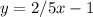`y = 2/5x -1` is written in slope-intercept form.

This formula looks like:

`y=mx+b`

where:

• M = Slope
• x = independent variable
• b = y-intercept

So:

• 
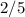  `2/5` is our slope
• 
  `x` remains our independent variable
• 
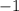  `-1` is our y-intercept.

1 ). For two lines to be parallel they must have the same slope.

• Slope would remain 2/5

2 ). For two line to be perpendicular they must have slopes that are opposite reciprocals.

• . Slope would become -5/2

As the question states, we must find the slope of a line parallel to the equation given. This means that the slope will remain 2/5.

Lets check our work!

Choose a random ordered pair. I will choose (5, 6).

Now, using point slope-form we can find out if what was said above is true!

This formula looks like:

`y - y1 = m (x-x1)`

Let us substitute:

`y - 6 = 2/5(x-5)`

Distribute:

`y-6=2/5x-2`

Add 6 to both sides:

`y= 2/5x+4`

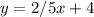
Now using both equations I will plot them on a graph to see if they a parallel.

As you can see from the graph below, these lines are parallel. Where the equation you were given is in blue and the equation I made is in red.

Based on all of the evidence, the slope will be 2/5.

Hope this helped! :)