Question

Please help me answer this question

Answer 1

• modulus: 3√2
• argument: -3π/4 (or 5π/4)

Explanation:

The modulus is the magnitude of the complex number; the argument is its angle (usually in radians).

__

rectangular form

The complex number can be cleared from the denominator by multiplying numerator and denominator by its conjugate:

`(-9+3i)/(1-2i)=((-9+3i)(1+2i))/((1-2i)(1+2i))=(-9+3i-18i-6)/(1+4)=-3-3i`

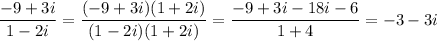
polar form

The magnitude of this number is the root of the sum of the squares of the real and imaginary parts:

modulus = √((-3)² +(-3)²) = 3√2

The argument is the arctangent of the ratio of the imaginary part to the real part, taking quadrant into consideration.

arg = arctan(-3/-3) = -3π/4 or 5π/4 . . . . radians

__

modulus∠argument = (3√2)∠(-3π/4)