Answer:
(a) width = (x - 1)
length = (7x - 6)
(b) Area = 350 cm²
Perimeter = 114 cm
Explanation:
Part (a)
Given equation:
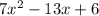
⇒ a = 7, b = -13, c = 6
Find 2 two numbers that multiply to ac and sum to b: -6 and -7
Rewrite b as the sum of these 2 numbers:
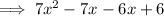
Factorize the first two terms and the last two terms separately:
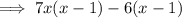
Factor out the common term (x - 1):
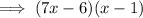
Therefore:
- width = (x - 1)
- length = (7x - 6)
Part (b)
Substitute the given value of x = 8 into the equations to find the area and perimeter:
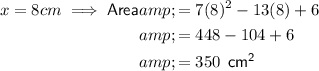
![\begin{aligned}\textsf{Perimeter} & = 2(\sf width+length)\\& =2[(x-1)+(7x-6)]\\ & = 2[(8-1)+(7(8)-6)]\\ & = 2[7+(56-6)] \\& = 2(7+50)\\& = 2(57)\\ & = 114 \sf \:\: cm\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wda50i3a4q50hzub5onafe4iuob6enzja0.png)