Answer:
Explanation:
The quadratic is
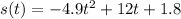
where s(t) is the height of the ball after a certain amount of time goes by. If we are looking for how long til it hits the ground, we know 2 things from that question. First we know that the height of an object on the ground is 0, and we also know that t is the time that the ball is in the air. Because the height of the ball when it's on the ground is 0, we will set s(t) equal to 0 and factor the quadratic to solve for t, the time the ball is in the air. Throw it into the quadratic formula to find those times.
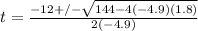 which will simplify to
which will simplify to
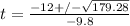
The 2 solutions we get from that are that
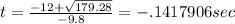 and
and
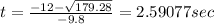
Now, the 2 things in math that will never be negative are distances and time, so we will disregard the negative time and go with t = 2.59 seconds. Not sure to where you need to round.