Answer:
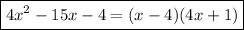
Solution Steps:
______________________________
1.) Change the equation using factored transformation:
- Quadratic polynomial can be factored using the transformation
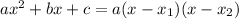 , where
, where
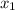 and
and
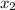 are the solutions of the quadratic equation
are the solutions of the quadratic equation
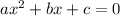 .
.
- This steps basically means change you current equation using the formula
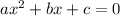 .
.
2.) Turn the factored form into the quadratic equation form:
- All equations of the form
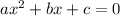 can be solved using the quadratic formula:
can be solved using the quadratic formula:
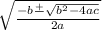 .
.
- The quadratic equation formula gives two solutions, one when
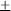 is addition and one when it is subtraction.
is addition and one when it is subtraction.
3.) Square -15:
Equation at the end of Step 3:
4.) Multiply −4 times 4:
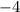 ×
×
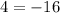
Equation at the end of Step 4:
5.) Multiply −16 times −4:
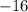 ×
×
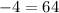
Equation at the end of Step 5:
6.) Add 225 to 64:
Equation at the end of Step 6:
7.) Take the square root of 289:
Equation at the end of Step 7:
8.) Change -15 to positive 15:
Equation at the end of Step 8:
9.) Multiply 2 by 4:
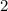 ×
×
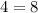
Equation at the end of Step 9:
10.) Now Solve:
Now solve the equation
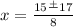 when
when
 is plus.
is plus.
Add 15 to 17:
Divide 32 by 8:
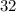 ÷
÷
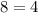
Now solve the equation
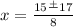 when
when
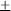 is minus.
is minus.
Subtract 15 by 17:
Reduce the fraction to lowest terms by extracting and canceling out 2:
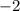 ÷
÷
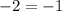
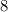 ÷
÷
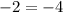
11.) Factor the expression:
Factor the original expression using
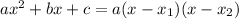 . Substitute 4 for
. Substitute 4 for
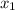 and
and
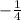 for
for
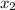 :
:
Simplify all the expressions of the form
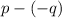 to
to
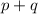 :
:
Add
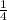 to x by finding a common denominator and adding the numerators. Then reduce the fraction to lowest terms if possible:
to x by finding a common denominator and adding the numerators. Then reduce the fraction to lowest terms if possible:
Cancel out 4, the greatest common factor in 4 and 4:
______________________________