

‣ Angle A = 5x - 60°
‣ Angle B = 2x + 40°
‣ Angle C = 3x - 80°

‣ The value of


By angle sum property [ASP] of a triangle which states that the sum of all angles of a triangle = 180°
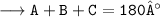
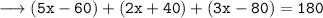
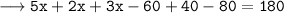
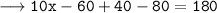
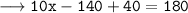
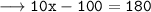
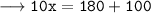
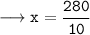
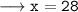
Therefore, the value of
 is 28°
is 28°


‣ Line p is parallel to line q which is intersected by a transversal.

‣ The unknown angles.

Finding angle

[linear pair axiom]
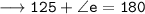
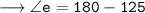
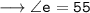
Now,
For angle
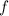
[Vertically opposite angles]
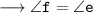
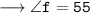
Now,
For angle

[Corresponding angles]
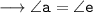
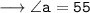
Now,
For angle
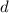
[Corresponding angles]
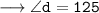
Now,
For angle

[Vertically opposite angles]
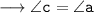
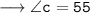
Now,
For angle
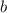
[Vertically opposite angles]
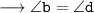
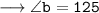
Hence,
★ Angle A = 55°
★ Angle B = 125°
★ Angle C = 55°
★ Angle D = 125°
★ Angle E = 55°
★ Angle F = 55°
