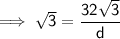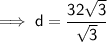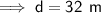Question

The angle of elevation of the top of a radio mast from a point due east of it and 96 m away from its base is 30°. From another point, due west of the mast, the angle of elevation of the top is 60°. Calculate the distance of the second point from the base of the mast.​

Answer 1

32 m

Explanation:

Trigonometric ratios

`\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)`

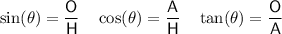
where:

• 
  `\theta` is the angle
• O is the side opposite the angle
• A is the side adjacent the angle
• H is the hypotenuse (the side opposite the right angle)

Calculate the height of the radio mast using the tan trig ratio.

Given:

• 
  `\theta` = 30°
• O = h (height of radio mast)
• A = 96 m

`\implies \sf tan(30^(\circ))=( \sf h)/(96)`

`\implies \sf h=96 \tan (30^(\circ))`

`\implies \sf h=(96 √(3))/(3)`

`\implies \sf h=32 √(3)\:\:m`

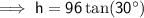
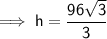
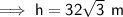
To calculate the distance from the second point to the base of the mast, use the tan trig ratio:

Given:

• 
  `\theta` = 60°
• O = 32√3 m
• A = d

`\implies \sf tan(60^(\circ))=( \sf 32 √(3))/(d)`

`\implies \sf √(3)=( \sf 32 √(3))/(d)`

`\implies \sf d=( \sf 32 √(3))/(√(3))`

`\implies \sf d=32\:\: m`