Answer:
B
Explanation:
To determine if a sequence is geometric, the terms need to have a common ratio. This means that to get from one term to the next, you need to multiply by the same number. Here's an example geometric sequence:
1) 2, 4, 8, 16, 32...
2) 4, 6, 9...
As you can see, to get from one term to the next in both of these sequences, you need to multiply by a certain number [the common ratio]. In sequence one, this number is 2. You need to multiply a term by 2 to get to the next term. In the second sequence, this number is 3/2. To find this certain number/common ratio, you can set the terms into ratios:
9/6=3/2
6/4=3/2
This ratio between the terms we get is the common ratio. Multiplying by this number will get you to the next term.
In this case [-4, -1, 1, -4...]:

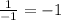
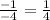
The ratios produced by the terms clearly aren't the same here, so the sequence is not geometric.