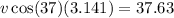Question

A ball is thrown from a top of a building of height 20m. If the initial velocity of the ball is 15m/s at 370 above the horizontal find, a) the velocity of the ball at 2s. b) the position at which the ball strike the ground.​

Answer 1

Step-by-step explanation:

Givens:

`h = 20 \: m`

`v _(ix) = 15 \cos(37) = 11.97`

`v _(iy) = 15 \sin(37) = 9.03`

`a _(y) = - 9.8`

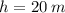
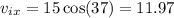
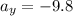
Let t=2 be the final velocity. Since Velocity stays the same horizontal , acceleration due to gravity changes the vertical direction

Use this equation

`v _(y) = v _(iy) + a _(y)(t)`

Plug in the knowns

`v _(y) = 15 \sin(37) +2 ( - 9.8)`

`v _(y) = - 10.57`

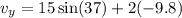
So the velocity in the y direction at 2 seconds is -10.57

The velocity in the x direction at 2 seconds is 11.97

Use the Pythagorean theorem to find the total velocity

`v = \sqrt{( - 10.57) {}^(2) + (11.97) {}^(2) }`

`v = 15.97`

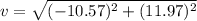
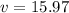
b. The range at which it strike the ground.

We need to find when the velocity at the top is zero.

Using the y direction,

`0 = v \sin( 37 ) - 9.8(t)`

`t = 0.921`

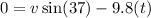
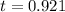
Next, find the height of the max.

`h = (1)/(2) ( 9.8)(0.921) {}^(2) = 4.16`

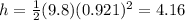
So the total distance is 4.16+20= 24.16

Next to find the total time it falls

`24.16 = (1)/(2) (9.8) {t}^(2)`

`t = 2.2`

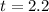
So our total flight time is

`3.141`

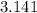
Range is

`v \cos(37) (3.141) = 37.63`