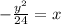1 Answer

THpubs · Answer 1 · 2023-10-01T18:46:29+0000

Explanation:

Notice the vertex and focus have the same y coordinate so this means we will have sideways parabola.

Equation of a sideways parabola is

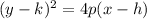
$(y - k) {}^(2) = 4p(x - h)$

Since the vertex is (0,0), we can get rid of h and k.

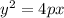
${y}^(2) = 4px$

Next Section: Value of P:

The value of P is the displacement between the focus and vertex.

So we do

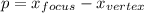
p = x _(focus) - x _(vertex)

p = - 6 - 0

p = - 6

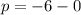
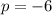
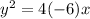
${y}^(2) = 4( - 6)x$

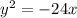
${y}^(2) = - 24x$

or

$- \frac{ {y}^(2) }{24} = x$

Please log in or register to add a comment.