Question

The product of two positive consecutive integers is 24 more than 6 times the first number.

What is the product of the two integers?

Answer 1

The product of two integers is 72.

Explanation:

Let,

x and x+1 be the two consecutive positive integers.

According to given statement;

The product of two positive consecutive integers is 24 more than 6 times the first number.

x(x+1) = 6x+24

`x^2+x=6x+24\\x^2+x-6x-24=0\\x^2-5x-24=0\\x^2-8x+3x-24=0\\x(x-8)+3(x-8)=0\\(x-8)(x+3)=0\\`

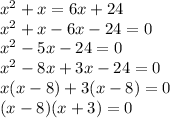
Either,

x-8 = 0

x=8

Or,

x+3 = 0

x=-3

As the integer is positive, therefore, the two integers are 8 and 9.

Product of two integers = 8*9 = 72

Hence,

The product of two integers is 72.