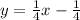Answer:
Explanation is written below.
Explanation:
1)
Given the line
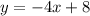
Comparing with the slope-intercept form of the line equation

Where m is the slope and b is the y-intercept
So, the slope of the line = m = -4
- We know that the parallel lines have equal slopes.
Thus, the equation of the line that is parallel to y = -4x + 8 and passes through the point (5, 1), using point slope form

Here, m is the slope and (x₁, y₁) is the point
substituting the values m = -4 and the point (5, 1)

y-1 = -4 (x - 5)
y-1 = -4x+20
y = -4x+20+1
y = -4x + 21
2)
Given the equation
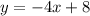
Comparing with the slope-intercept form of the line equation

Where m is the slope and b is the y-intercept
So, the slope of the line = m = -4
As we know that the slope of the perpendicular line is basically the negative reciprocal of the slope of the line, so
The slope of the perpendicular line will be: 1/4
Thus, an equation of the line that is perpendicular to y = -4x + 8 and passes through the point (5,1), using point slope form

Here, m is the slope and (x₁, y₁) is the point
substituting the values m = 1/4 and the point (5, 1)
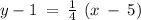
Add 1 to both sides