Question

A store is having a sale on walnuts and chocolate chips. For 4 pounds of walnuts and 8 pounds of chocolate chips, the total cost is $25. For 2 pounds of walnuts and 3 pounds of chocolate chips, the total cost is $10. Find the cost for each pound of walnuts and each pound of chocolate chips.

Answer 1

The cost of each pound of walnuts is $1.25 and each pound of chocolate chips is $2.50

Explanation:

Let,

x be the price per pound of walnuts

y be the price per pound of chocolate chips

According to given statement,

4x+8y=25 Eqn 1

2x+3y=10 Eqn 2

Multiplying Eqn 2 by 2

2(2x+3y=10)

4x+6y=20 Eqn 3

Subtracting Eqn 3 from Eqn 1

(4x+8y)-(4x+6y)=25-20

4x+8y-4x-6y=5

2y=5

Dividing both sides by 2

`(2y)/(2)=(5)/(2)\\y=2.50`

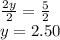
Putting y=2.50 in Eqn 2

2x+3(2.50)=10

2x+7.50=10

2x=10-7.50

2x=2.50

Dividing both sides by 2

`(2x)/(2)=(2.50)/(2)\\x=1.25`

Hence,

The cost of each pound of walnuts is $1.25 and each pound of chocolate chips is $2.50