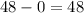Question

Find the area bounded by the graphs of the indicated equations over the given interval.

y=x²-25; y = 0; -3≤x≤0

Answer 1

48

Explanation:

`y = 0`

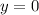
is basically the horizontal axis.

First, find the integral of x^2-25.

Remember that

integral of a constant is that constant times x.

Also that

to take the integral of a power function, add 1 to the degree and divide by that same degree.

`y = {x}^(2) - 25`

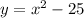
We then get

`\frac{ {x}^(3) }{3} - 25x`

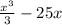
Evaluate at -3

`\frac{ - 3 {}^(3) }{3} - 25( - 3)`

`- 27 + 75 = 48`

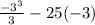
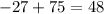
Then we evaluate at 0

`\frac{0 {}^(3) }{3} - 25(0) = 0`

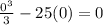
Next, we subtract the the answer then we get

`48 - 0 = 48`