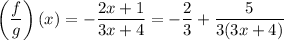These are all abbreviated ways of writing a sum or product of functions.
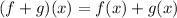
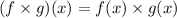
Given
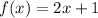 and
and
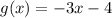 , we have
, we have
a)
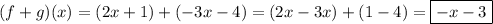
b)
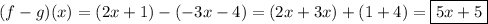
c) same as (b), but I bet you meant to use some other symbol. I'll just assume multiplication:

d)
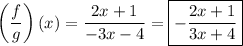
though you could go on to simplify the quotient via long division; you would end up with the equivalent function (assuming x ≠ -4/3)