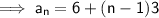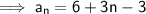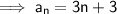Answer:
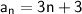
Explanation:
An explicit formula for an arithmetic sequence allows you to find the nth term of the sequence.
A recursive formula for an arithmetic sequence allows you to find the nth term of the sequence provided you know the value of the previous term in the sequence.
Explicit formula
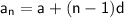
where:
 is the nth term
is the nth term- a is the first term
- n is the number of the term
- d is the common difference
Given:
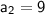
- d = 3
- n = 2
Substituting these values into the formula to find a:
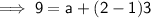

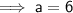
Therefore the formula is: