Question

Mang Jose plans to fence his rectangular lot before he will plant mushrooms for his mushrooms production business. The perimeter of the lot is 40 meters and the area is 96 square meters.

Using the concept of the sum and product of roots of a quadratic equation, how would you determine the length and the width of the rectangular lot? Provide a quadratic equation representing this scenario.


Someone help me

Answer 1

Answer: The rectangular lot is 12x8 meters

Explanation: Perimeter of a geometric figure is the sum of all its sides.

A rectangle is a quadrilateral that has opposite sides parallel and equal, which means, and suppose l is length and w is width:

P = 2l + 2w

The perimeter of the lot is 40m, thus:

2l + 2w = 40

Area of a rectangle is calculated as:

A = length x width

The lot has area of 96, thus:

lw = 96

Solving the system of equations:

2l + 2w = 40 (1)

lw = 96 (2)

Isolate l from (1):

2l = 40 - 2w

l = 20 - w (3)

Substitute (3) in (2):

w(20-w) = 96

`-w^(2)+20w=96`

`-w^(2)+20w-96=0`

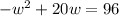
There are many methods to determine the roots of a quadratic equation. One of them is using the sum and product of those roots.

• Sum of the roots is given by:

`sum = (-b)/(a)`

`sum=(-20)/(-1)`

sum = 20

• Product of the roots is:

`prod=(c)/(a)`

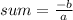
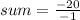
`prod=(-96)/(-1)`

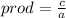
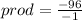
prod = 96

The roots of the quadratic equation are numbers which the sum results in 20 and product is 96:

w₁ = 12

w₂ = 8

If we substitute w to find l, the numbers will be l₁ = 8 and l₂ = 12.

Since length is bigger than width, the rectangular lot Mang Jose has to plant mushrooms measures 12m in length and 8m in width