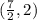Answer:
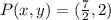
Explanation:
Given
Parallelogram LMNO
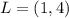
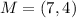
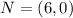
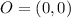
Required
Determine the point of intersection
The point of intersection of the diagonal is the midpoint of the parallelogram.
The diagonals are: LN and MO
Calculating midpoint, P of LN
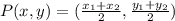
Where
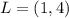 ---
---

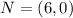 ---
---

So:
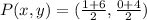
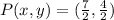
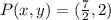
To confirm, we make use of diagonals MO
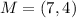 ---
---

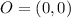 ---
---

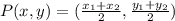
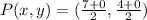
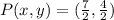
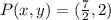
Hence, the coordinates of the intersection, P is