Question

A red candle is 8 inches tall and burns at a rate of 7/10 inch per hour.A blue candle is 6 inches tall and burns at a rate of 1/5 inch per hour. After how many hours will both candles be the same hight?

Answer 1

4 hours

Explanation:

Given that:

Initial height of red candle = 8 inches

Rate of burning of red candle =
`(7)/(10)\ inch/hr`

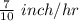
Initial height of blue candle = 6 inches

Rate of burning of blue candle =
`(1)/(5)\ inch/hr`

To find:

Time taken in hours such that both the candles have the same height.

Solution:

Let the time taken such that both the candles have the same height =
`t` hours

Height of red candle after
`t` hours =
`(8 - (7)/(10)t) \ inches`

Height of blue candle after
`t` hours =
`(6 - (1)/(5)t) \ inches`

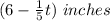
Writing both the expressions as equal:

`8-(7)/(10)t=6-(1)/(5)t\\\Rightarrow 8-6=(7)/(10)-(1)/(5)t\\\Rightarrow 2 = ((7-2)/(10))t\\\Rightarrow (5t)/(10)=2\\\Rightarrow t=4\ hours`

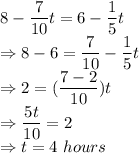
After 4 hours, height of both the candles will be same.