Question

The ratio of 14C to 12C in living organisms is 1.3 × 10-12. The fossilized remains of an organism are discovered and the ratio of 14C to 12C in the fossil is measured to be 4.6 × 10-13. How long ago, in years was the organism alive? (The half life of 14C is 5,730 years.)

Answer 1

t = 8588 years

Explanation:

From the given information:

Using the formula:

`k = (In (2))/(t_(1/2))`

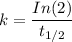
Given that:

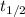`t_(1/2)` = 5730 years

Then:

`k = (In (2))/(5730)`

`k = (0.6931472)/(5730)`

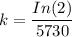
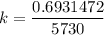
k = 1.20968 × 10⁻⁴

However; the expression to find the value of x is:

`x= x_oe^(-kt)`

`4.6 * 10^(-13) = 1.3 * 10^(-12) * e^{(-1.20968* 10^(-4) * t)}`

`(4.6 * 10^(-13) )/(1.3 * 10^(-12))= e^{(-1.20968* 10^(-4) * t)}`

`0.353846= e^{(-1.20968* 10^(-4) * t)}`

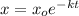
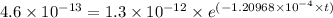
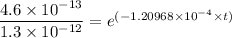
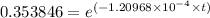
(-1.20968 × 10⁻⁴ × t) = In(0.353846)

(-1.20968 × 10⁻⁴ × t) = -1.03889

`t = (-1.03889)/(-1.20968 * 10^(-4))`

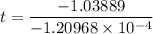
t = 8588 years