Answer:
a) Number of projects in the first year = 90
b) Earnings in the twelfth year = $116500
Total money earned in 12 years = $969000
Explanation:
Given that:
Number of projects done in fourth year = 129
Number of projects done in tenth year = 207
There is a fixed increase every year.
a) To find:
Number of projects done in the first year.
This problem is nothing but a case of arithmetic progression.
Let the first term i.e. number of projects done in first year =

Given that:
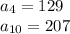
Formula for
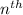 term of an Arithmetic Progression is given as:
term of an Arithmetic Progression is given as:

Where
 will represent the number of projects increased every year.
will represent the number of projects increased every year.
and
 is the year number.
is the year number.
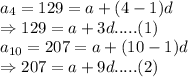
Subtracting (2) from (1):
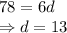
By equation (1):
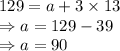
Number of projects in the first year = 90
b)
Number of projects in the twelfth year =
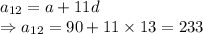
Each project pays $500
Earnings in the twelfth year = 233
 500 = $116500
500 = $116500
Sum of an AP is given as:
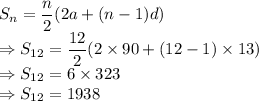
It gives us the total number of projects done in 12 years = 1938
Total money earned in 12 years = 500
 1938 = $969000
1938 = $969000