Question

The first two terms in an arithmetic progression are -2 and 5. The last term in the progression is the only number in the progression that is greater than 200. Find the sum of all the terms in the progression.

Answer 1

Given:

The first two terms in an arithmetic progression are -2 and 5.

The last term in the progression is the only number in the progression that is greater than 200.

To find:

The sum of all the terms in the progression.

Solution:

We have,

First term :
`a=-2`

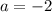
Common difference :
`d = 5 - (-2)`

`= 5 + 2`

`= 7`

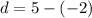
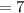
nth term of an A.P. is

`a_n=a+(n-1)d`

where, a is first term and d is common difference.

`a_n=-2+(n-1)(7)`

According to the equation,
`a_n>200`.

`-2+(n-1)(7)>200`

`(n-1)(7)>200+2`

`(n-1)(7)>202`

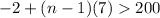
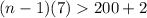
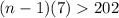
Divide both sides by 7.

`(n-1)>28.857`

Add 1 on both sides.

`n>29.857`

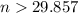
So, least possible integer value is 30. It means, A.P. has 30 term.

Sum of n terms of an A.P. is

`S_n=(n)/(2)[2a+(n-1)d]`

Substituting n=30, a=-2 and d=7, we get

`S_(30)=(30)/(2)[2(-2)+(30-1)7]`

`S_(30)=15[-4+(29)7]`

`S_(30)=15[-4+203]`

`S_(30)=15(199)`

`S_(30)=2985`

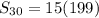
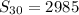
Therefore, the sum of all the terms in the progression is 2985.