Question

Un niño de 25 kg corre por un jardín con una velocidad de 2.5 m/s de forma que su trayectoria es tangente al borde de un carrusel de 500 kg•m2 de momento de inercia y un radio de 2 m, que está parado. El niño salta sobre el carrusel y lo pone en movimiento. Determina la velocidad angular del niño y del carrusel cuando se mueven juntos.

Grupo de opciones de respuesta:


0.25 rad/s


5 rad/s


0.208 m/s


0.208 rad/s

Answer 1

La velocidad angular del niño y del carrusel cuando se mueven juntos es 0.208 radianes por segundo.

Step-by-step explanation:

Asumamos que tanto el niño como el carrusel no tienen carga externa aplicada sobre aquellos, de modo que se puede aplicar el Principio de Conservación de la Cantidad de Movimiento Angular:

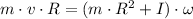`m\cdot v \cdot R = (m\cdot R^(2)+I)\cdot \omega` (1)

Donde:

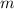`m` - Masa del niño, medida en kilogramos.

`v` - Velocidad lineal inicial del niño, medida en metros por segundo.

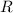`R` - Radio máximo del carrusel, medida en metros.

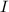`I` - Momento de inercia del carrusel, medida en kilogramo-metros cuadrados.

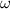`\omega` - Velocidad angular final del sistema niño-carrusel, medida en radianes por segundo.

Si sabemos que
`m = 25\,kg`,
`v = 2.5\,(m)/(s)`,
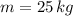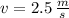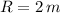`R = 2\,m` y
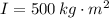`I = 500\,kg\cdot m^(2)`, tenemos que la velocidad angular final es:

`\omega = (m\cdot v\cdot R)/(m\cdot R^(2)+I)`

`\omega = ((25\,kg)\cdot \left(2.5\,(m)/(s) \right)\cdot (2\,m))/((25\,kg)\cdot (2\,m)^(2)+500\,kg\cdot m^(2))`

`\omega = 0.208\,(rad)/(s)`

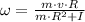
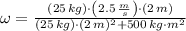
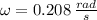
La velocidad angular del niño y del carrusel cuando se mueven juntos es 0.208 radianes por segundo.