Question

Your boss at the Cut-Rate Cuckoo Clock Company asks you whatwould happen to the frequency of the angular SHM of the balancewheel if it had the same density and the same coil spring (thus thesame torsion constant), but all the balance wheel dimensions weremade one-third as great to save material.

a)By what factor would the frequency change?

b)Would the frequency increase or decrease by the factor foundin part (a)?

c)By what factor would the torsion constant need to be changedto make the smaller balance wheel oscillate at the originalfrequency?

d)Would the torsion constant need to be increased or decreasedby the factor found in part (c)?

Answer 1

a) the factor between the frequencies is f ’/ f₀ = 9

b) the frequency increases f ’= 9 f₀

c) So that the frequency is equal to the initial one k ’= k₀ / 81

d) the torque constant must decrease

Step-by-step explanation:

This is a simple harmonic motion, like angular velocity

w =
`\sqrt{(k)/(I) }`

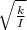
where k is the torsion constant and I the moment of inertia of the flywheel.

Angular velocity and frequency are related

w = 2π f

we substitute

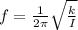`f= (1)/(2\pi ) \sqrt{(k)/(I) }` (1)

We will use the subscript o for the system without change

f =
`(1)/(2\pi )`
`\sqrt{(k)/(I_(o) ) }`

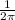
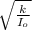
In the problem they indicate that the torsion constant remains constant, therefore we must analyze the moment of inertia, in general the flywheels are circular discs,

I = ½ M R²

Let's find the change when reducing the radius r ’= r / 3

Let's use the density

ρ = m ’/ V’

m ’= ρ V’

disk volume is

V = π r² e

suppose that the thickness is small and does not change, substitute

m ’= ρ π
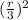`((r)/(3)) ^(2)` e = 1/9 m

Moment of inertia

I ’= ½ m’ r’²

I ’=
`(1)/(2)`
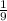`(1)/(9)` m (\frac{r}{3}) ^{2} = 1/81 (½ m r²)

I ’= 1/81 Io

we substitute in equation 1

f ’=
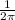`(1)/(2\pi )` \sqrt{\frac{k}{I} }

f ’= \frac{1}{2\pi } \sqrt{\frac{81k}{Io} }

f ’= 9 f₀

Let's analyze the questions

a) the factor between the frequencies is

f ’/ f₀ = 9

b) the frequency increases

f ’= 9 f₀

c) So that the frequency is equal to the initial one

k ’= k₀ / 81

d) the torque constant must decrease