Question

A transverse, sinusoidal wave travels in a string and can be described by the function: y(x,t)=0.87 sin(21x−4.9t). What is the speed of this wave?

Answer 1

2.61m/s

Step-by-step explanation:

Given the wave function;

y(x,t)=0.87 sin(21x−4.9t).

The general wave equation is expressed as;

`y = Asin(2\pi ft + 2\pi x /\lambda)`

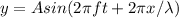
f is the frequency of the wave

t is the time

`\lambda\\` is the wavelength

On comparing;

2πft = 4.9t

2πf= 4.9

f = 4.9/2π

f = 4.9/2(3.14)

f = 4.9/6.28

f = 0.78Hz

Get the wavelength;

2πx/
`\lambda` = 21x

2π/
`\lambda` = 21

2π = 21
`\lambda`

`\lambda` = 21/2π

`\lambda` = 21/2(3.14)

`\lambda` = 21/6.28

`\lambda` = 3.34m

Speed = frequency * wavelength

Speed of the wave = 0.78 * 3.34

Speed of the wave = 2.61m/s

Hence the speed of the wave is 2.61m/s