Question

PLEASE SOMEONE HELP I TRULY DO NOT UNDERSTAND

Find F^-1(x), the inverse of F(x).

f(x)-9x^3-4
Show your work please because I don’t understand.

Answer 1

9514 1404 393

Answer:

`f^(-1)(x)=\frac{\sqrt[3]{3x+12}}{3}`

Explanation:

For function ...

`y=f(x)`

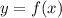
sometimes we know y, but we want to find the corresponding value x. That is, we would like to have an inverse function:

`x=f^(-1)(y)`

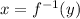
Here, I have said the input to the inverse function is the value of y for which we want the corresponding value of x.

__

Normally, we write the inverse function basically the same way we write the function. The input is named x, and the output is named y. We can swap the variable names for input and output either before or after we find the equation that relates them.

Perhaps you can see that finding the inverse function

`x=f^(-1)(y)`

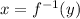
amounts to solving the function relation y = f(x) for x. If we interchange variables first, it is the same as solving x = f(y) for y.

__

To find the inverse, we can interchange the variables and solve for y.

`x=f(y)=9y^3-4\\\\x+4=9y^3\qquad\text{add 4}\\\\(x+4)/(9)=y^3\qquad\text{divide by 9}\\\\(3x+12)/(27)=y^3\qquad\text{make the denominator a cube; multiply by 3}\\\\y=\frac{\sqrt[3]{3x+12}}{3}\qquad\text{take the cube root}\\\\\boxed{f^(-1)(x)=\frac{\sqrt[3]{3x+12}}{3}}`

_____

The graph of the inverse of a function is the reflection of the graph of the function across the line y=x. The given function and the inverse we found are graphed in the attachment. The dashed line is y=x.