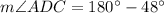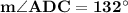Question

Type the correct answer in the box. Round your answer to the nearest integer.

B
D
30
35
A
С
In the figure, if m_ABD = 120°, then m_ADC =
-4345

Answer 1

`m\angle ADC=132^\circ`

Explanation:

The Law of Sines

It is an equation relating the lengths of the sides of a triangle to the sines of its opposite angles. If A, B, and C are the lengths of the sides and a,b,c are their respective opposite angles, then:

`\displaystyle (A)/(\sin a)=(B)/(\sin b)=(C)/(\sin c)`

We have completed the figure with the variable x for angle BDA. Thus

`\displaystyle (35)/(\sin 120^\circ)=(30)/(\sin x)`

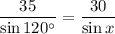
Solving for x:

`\displaystyle \sin x=(30\sin 120^\circ)/(35)`

Calculating:

`\sin x=0.742`

`x=\arcsin 0.742`

`x\approx 48^\circ`

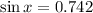
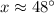
Since angles ADC and x are linear, their sum is 180° and:

`m\angle ADC=180^\circ-48^\circ`

`\mathbf{m\angle ADC=132^\circ}`