Answer:
a. The slope of EK is

b. The equation of line EK is y =
 x -
x -

Explanation:
The form of the equation of a line is y = m x + b, where
- m is the slope of the line
The rule of the slope is m =
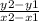 , where
, where
- (x1, y1) and (x2, y2) are two points on the line
- The rule of the mid-point is (
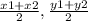 )
)
∵ BECK is a rhombus
∵ The diagonal is the line that joins two opposite vertices
∵ B and C are opposite vertices in the rhombus
∵ E and K are opposite vertices in the rhombus
∴ BC and EK are the diagonals of the rhombus BECK
∵ The diagonals of the rhombus are ⊥ and bisect each other
∴ EK is ⊥ bisector to BC
→ Let us find the slope and the mid-point of BC
∵ B = (3, 5) and C = (7, -3)
∴ x1 = 3 and y1 = 5
∴ x2 = 7 and y2 = -3
→ Substitute them in the rule of the slope above to find it
∵ m =
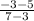 =
=
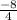 = -2
= -2
∴ m = -2
∴ The slope of BC = -2
→ To find the slope of EK reciprocal the slope of BC and change its sign
∴ m⊥ =

∴ The slope of EK =

a. The slope of EK is

→ Substitute the value of the slope in the form of the equation above
∵ y =
 x + b
x + b
→ To find b substitute x and y in the equation by the coordinates
of a point on the line
∵ The mid-point of BC is the mid-point of EK
∵ The mid-point of BC = (
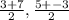 ) = (
) = (
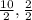 ) = (5, 1)
) = (5, 1)
∴ The mid-point of EK = (5, 1)
→ Substitute x by 5 and y by 2 in the equation
∵ 1 =
 (5) + b
(5) + b
∴ 1 =
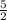 + b
+ b
→ Subtract
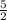 from both sides
from both sides
∴
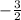 = b
= b
→ Substitute the value of b in the equation
∵ y =
 x +
x +
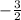
∴ y =
 x -
x -

b. The equation of line EK is y =
 x -
x -
